Seq2Seq Learning Part C: Basic Encoder-Decoder Architecture & Design

Welcome to the Part C of the Seq2Seq Learning Tutorial Series. In this tutorial, we will design a Basic Encoder-Decoder model to solve the sample Seq2Seq problem introduced in Part A.

We will use LSTM as the Recurrent Neural Network layer in Keras.

You can access all my SEQ2SEQ Learning videos on Murat Karakaya Akademi Youtube channel in ENGLISH or in TURKISH

You can access all the tutorials in this series from my blog at www.muratkarakaya.net

If you would like to follow up on Deep Learning tutorials, please subscribe to my YouTube Channel or follow my blog on muratkarakaya.net. Thank you!

Photo by Med Badr Chemmaoui on Unsplash

REMINDER:

This is the Part C of the Seq2Seq Learning series.
Please check out the previous parts to refresh the necessary background knowledge in order to follow this part with ease.

A Simple Seq2Seq Problem: The reversed sequence problem

Assume that:

We are given a parallel data set including X (input) and y (output) such that X[i] and y[i] have some relationship

In that tutorial, I will generate X and y parallel datasets such that y sequence will be the reverse of the given X sequence. For example,

Given sequence X[i] length of 4:

X[i]=[3, 2, 9, 1]

Output sequence (y[i]) is the reversed input sequence (X[i])

y[i]=[1, 9, 2, 3]

I will call this parallel dataset: “the reversed sequence problem”

In real life (like Machine Language Translation, Image Captioning, etc.), we are given (or build) a parallel dataset: X sequences and corresponding y sequences

However, to set up an easily traceable example, I opt out to set y sequences as the reversed of X sequences
However, you can create X and y parallel datasets as you wish: sorted, reverse sorted, odd or even numbers selected, etc.
We use the parallel data set to train a seq2seq model which would learn
how to convert/transform an input sequence from X to an output sequence in y

IMPORTANT:

In the reversed sequence problem, the input & output sequence lengths are fixed and the same.
In PART E, we will change the problem and the solution such that we will be dealing with variable-length sequences after we built the encoder-decoder model.

Configure the problem

Number of Input Timesteps: how many tokens / distinct events /numbers/words etc in the input sequence
Number of Features: how many features/dimensions used to represent one token / distict events/numbers / word etc
Here, we use one-hot encoding to represent the integers.
The length of the one-hot coding vector is the Number of Features
Thus, the greatest integer will be the Number of Features-1
When the Number of Features=10 the greatest integer will be 9 and will be represented as [0 0 0 0 0 0 0 0 0 1]

Notes: 
1. For each input sequence (X), selecting  4  random numbers between 1 (inclusive) and  10  (exclusive)  2. 0 is reserved as the SART Symbol

A sample X 
X=[1, 9, 7, 7]

reversed input sequence (X) is the output sequence (y) 
y=[7, 7, 9, 1]

Each input and output sequences are converted one_hot_encoded format in  10  dimensions
X=[[0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 1 0 0]]
y=[[0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0 0 1]
 [0 1 0 0 0 0 0 0 0 0]]

Generated sequence datasets as follows (batch_size,time_steps, features)
X_train.shape:  (2000, 4, 10) y_train.shape:  (2000, 4, 10)
X_test.shape:  (200, 4, 10) y_test.shape:  (200, 4, 10)
time: 75.5 ms

Before starting, you need to know:

Python
Keras/TF
Deep Neural Networks
Recurrent Neural Network concepts
LSTM parameters and outputs
Keras Functional API

If you would like to refresh your knowledge about the above topics please check Murat Karakaya Akademi resources on YouTube / muratkarakaya.net.

BASIC ENCODER DECODER ARCHITECTURE/DESIGN

Why do we need a new architecture/design?

So far, we first train a model and then use that trained model in the prediction
However, this approach assumes that input and/or output sizes are fixed, known in advance, and not continuous
Moreover, this approach is not good at handling longer sequences
Furthermore, this approach needs more resources (more data, more training, more layers, etc.) to discover even the simple seq2seq relations

What are we looking for in the new design?

A flexible train and predict/inference process
The model should handle the variable size of input/output
Seq2Seq conversion should be done with reasonable resources and with high accuracy
The model should be scalable in terms of input/output size (long sequences)

How a Basic Encoder-Decoder Model solves Seq2Seq Learning Problem:

Conceptually, we have two main components working together in the model:

Encoder encodes the sequence input into a new representation
This representation is called Context/Toughth Vector
The decoder decodes the Context/Toughth Vector into an output sequence

Image taken from here

Note 1: There are other proposed methods to solve seq2seq problems such as Convolution models or Reinforcement methods.

Note 2: In this tutorial we focus on using Recurrent Neural Networks in Enoder- Decoder architecture. We will use LSTM as the Recurrent Neural Network

Key Concepts

Training: During training, we train the encoder and decoder such that they work together to create a context (representation) between input and output
Inference (Prediction): After learning how to create the context (representation), they can work together to predict the output
Encode all- decode one at a time: Mostly, the encoder reads all the input sequence and create a context (representation) vector. Decoder use this context (representation) vector and previously decoded results to create new output step by step.
Teacher forcing: During training decoder receives the correct output from the training set as the previously decoded result to predict the next output. However, during inference decoder receives the previously decoded result to predict the next output. Teacher forcing improves the training process.

NOTE: We will cover Teacher forcing in the next part

DO NOT WORRY! WE WILL SEE ALL THE ABOVE CONCEPTS IN ACTION BELOW!

Quick LSTM reminder:

LSTM has 3 important parameters (for the time being!)

units: Positive integer, the dimensionality of the output space
return_sequences: Boolean, whether to return the last output. in the output sequence, or the full sequence. Default: False.
return_state: Boolean, whether to return the last state in addition to the output. Default: False.

The first parameter (units) indicates the dimension of the output vector/matrix.

The last 2 parameters (return_sequences and return_state) determine what the LSTM layer outputs. LSTM can return 4 different sets of results/states according to the given parameters:

Default: Last Hidden State (Hidden State of the last time step)

2. return_sequences=True : All Hidden States (Hidden State of ALL the time steps)

3. return_state=True : Last Hidden State+ Last Hidden State (again!) + Last Cell State (Cell State of the last time step)

4. return_sequences=True + return_state=True: All Hidden States (Hidden State of ALL the time steps) + Last Hidden State + Last Cell State (Cell State of the last time step)

Using these 4 different sets of results/states, we can stack LSTM layers in various ways!

IMPORTANT: If you are not familiar with LSTM, you would like to consider refreshing your knowledge by watching/reading below resources:

Videos:

LSTM: From A Programmer’s Perspective

Notebooks:

IMPORTANT: USE OF FUNCTIONAL KERAS API:

In order to implement the Encoder-Decoder approach, we will use Keras Functional API to create train & inference models
Thus, ensure that you are familiar with Keras Functional API

1. Understand & apply context vector

Context vector is

the encoded version of the input sequence
the new representation of the input sequence
the summary of the input sequence
the last (hidden & cell) states of the encoder
the initial (hidden & cell) states of the decoder But,
NOT the output of the encoder

Therefore, in the encoder LSTM we will use return_state=True for getting the last Hidden and Cell states.

Decide the context (latent) vector dimension

Actually, it is the number of LSTM units parameter of the LSTM layer in Keras.
As the context vector is the condensed representation of the whole input sequence mostly we prefer a large dimension.
We can increment the context (latent) vector dimension by 2 ways:
increment the number of units in encoder LSTM
and/or increment the number of encoder LSTM layers
For the sake of simplicity, we use a single LSTM layer in the encoder and decoder layers for the time being

So, let’s decide numberOfLSTMunits, in other words, the Output Dimension of the encoder

numberOfLSTMunits = 16

Define the Encoder by using LSTM layer

Notice that the output of the encoder is the last hidden states and cell states of the LSTM cell
return_states=True returns: Last Hidden State+ Last Hidden State (again!) + Last Cell State (Cell State of the last time step)
Since we will have the last hidden states twice, we can ignore the first one (actually this one is considered the output of the LSTM in general!).
In other words, we ignore the output of the encoder LSTM but use the last Hidden and Cell states.
That output is the context/thought (latent) vector
By using the context vector, we will set the initial states of the decoder LSTM.
That is, the decoder will start to function with the last state of the encoder

A Sample Encoder

Can you imagine the dimension of the context vector (states) for the below code?

# Define the encoder layers
encoder_inputs = Input(shape=(n_timesteps_in, n_features), name='encoder_inputs')
encoder_lstm = LSTM(numberOfLSTMunits, return_state=True,  name='encoder_lstm')
encoder_outputs, state_h, state_c = encoder_lstm(encoder_inputs)
states = [state_h, state_c]

As seen above, encoder LSTM with return_state=True returns 3 tensors:

last hidden state: encoder_outputs
last hidden state (again!): state_h
last cell state: state_c

The dimension of each state equals to the LSTM unit number (numberOfLSTMunits)

encoder_lstm.output_shape[(None, 16), (None, 16), (None, 16)]

Context vector generally is [state_h , state_c]. In the LSTM, these values are actually the last states of the encoder LSTM.

# Define and compile model first
model_encoder = Model(encoder_inputs, states) 
context_vector= model_encoder(X)
print('X.shape: ', X.shape)
print('numberOfLSTMunits: ', numberOfLSTMunits)
print(' last hidden states',context_vector[0].numpy().shape)
print(' last cell states',context_vector[1].numpy().shape)X.shape:  (1, 4, 10)
numberOfLSTMunits:  16
 last hidden states (1, 16)
 last cell states (1, 16)

Define the Decoder LSTM

We can use context vector, here [state_h , state_c], to initialize the decoder LSTM
We set up our decoder LSTM to return all hidden states, and to return cell states as well by setting return_sequences and return_state parameters to True

# Set up the decoder, which will only process one timestep at a time.
decoder_inputs = Input(shape=(1, n_features), name='decoder_inputs')
decoder_lstm = LSTM(numberOfLSTMunits, return_sequences=True, 
                    return_state=True, name='decoder_lstm')
decoder_dense = Dense(n_features, activation='softmax')

outputs, state_h, state_c = decoder_lstm(decoder_inputs,initial_state=states)decoder_lstm.output_shape[(None, 1, 16), (None, 16), (None, 16)]

Now decoder is ready to process the data: BUT WHICH DATA?
Input data is already consumed by Encoder and converted into a context vector.
A context vector is already consumed as initial states of the decoder (LSTM)
So what is the input for the decoder?
Remember the problem: reversing the input sequence. So we have input X any output y as below:

In raw format:
X=[1, 9, 7, 7]
y=[7, 7, 9, 1]

In one_hot_encoded format:
X=[[0 1 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0 1]
 [0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 1 0 0]]
y=[[0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 1 0 0]
 [0 0 0 0 0 0 0 0 0 1]
 [0 1 0 0 0 0 0 0 0 0]]

HOW ENCODER — DECODER WOULD WORK IN INFERENCE

Encoder:

Receives the input sequence
It consumes the tokens each time steps
After finishing all tokens in the input sequence, the Encoder outputs last hidden & cell states as the context vector.
Encoder stops

Decoder:

Decoder produces the output sequence one by one
For each output, the decoder consumes a context vector and an input
The initial context vector is created by the encoder
The initial input to the decoder is a special symbol for the decoder to make it start, e.g. ‘zero’
Using initial context and initial input, the decoder will generate/predict the first output
For the next time step, the decoder will use its own last hidden & cell states as a context vector and generated/predicted output at the previous time step as input
The decoder will work in such a loop using its states and output as the next step context vector and input until:
the generated output is a special symbol (e.g. ‘STOP’ or ‘END’) or
the pre-defined maximum steps (length of output) is reached.

REMINDER: TYPES OF SEQ2SEQ PROBLEMS:

According to the length of input & output sequences, these lengths can be fixed or variable
In the reversing input sequence problem, input & output sequence lengths are fixed and the same. We have n_timesteps_in tokens in input & output sequences.
Therefore, the decoder in our solution will stop after producing a pre-determined number of tokens (outputs). That is, we do not need ‘STOP’ or ‘END’ symbol in this problem.
However, the decoder will begin to work with ‘START’ symbol. We reserve the 0 (zero) as the ‘START’ symbol. Therefore, we DID NOT use 0 (zero) as a token while creating sequence samples.
In summary, we will condition the decoder to start with a context vector and ‘START’ symbol to predict the output sequence as many as n_timesteps_in parameter.

HOW TO TRAIN & TEST ENCODER — DECODER

We need 2 input sequences:

Input for encoder: encoder_inputs
Input for decoder: decoder_inputs

The encoder_inputs is given in the problem as a sequence. We will supply them directly to the Encoder.

Encoder:

receives the input sequence
consumes the tokens at each time steps
outputs last hidden & cell states as the context vector after finishing all tokens in the input sequence
stops

For decoder_inputs we will provide ‘START’ token as the initial input.

Decoder:

predicts the first-time step ouput consuming the context vector provided by Encoder and initial input.
consumes the predicted output as the next input, its previous last hidden & cell states as the context vector for the next time steps
stops when the required number of tokens generated, since, in our problem, input and output sequences have fixed and same sizes

CREATE A MODEL INCLUDING ENCODER & DECODER

Define A model in which

Encoder receives encoder input data and converts it to a context vector
The decoder runs in a loop:
The decoder is initialized with a context vector and receives decoder input data
Decoder converts decoder input data to one-time step output
The decoder also outputs its hidden states and cell states as the context vector
in the next cycle of the loop, the decoder uses its states and output as the input for itself (the context vector and the input)

IMPORTANT: You can access and run the full code on Colab.

def create_hard_coded_decoder_input_model(batch_size):
  # The first part is encoder
  encoder_inputs = Input(shape=(n_timesteps_in, n_features), name='encoder_inputs')
  encoder_lstm = LSTM(numberOfLSTMunits, return_state=True,  name='encoder_lstm')
  encoder_outputs, state_h, state_c = encoder_lstm(encoder_inputs)
  
  # initial context vector is the states of the encoder
  states = [state_h, state_c]
  
  # Set up the decoder layers
  # Attention: decoder receives 1 token at a time &
  # decoder outputs 1 token at a time 
  decoder_inputs = Input(shape=(1, n_features))
  decoder_lstm = LSTM(numberOfLSTMunits, return_sequences=True, 
                      return_state=True, name='decoder_lstm')
  decoder_dense = Dense(n_features, activation='softmax',  name='decoder_dense')

  all_outputs = []
  # Prepare decoder initial input data: just contains the START character 0
  # Note that we made it a constant one-hot-encoded in the model
  # that is, [1 0 0 0 0 0 0 0 0 0] is the initial input for each loop
  decoder_input_data = np.zeros((batch_size, 1, n_features))
  decoder_input_data[:, 0, 0] = 1 
  
  # that is, [1 0 0 0 0 0 0 0 0 0] is the initial input for each loop
  inputs = decoder_input_data
  # decoder will only process one time step at a time
  # loops for fixed number of time steps: n_timesteps_in
  for _ in range(n_timesteps_in):
      # Run the decoder on one time step
      outputs, state_h, state_c = decoder_lstm(inputs,
                                              initial_state=states)
      outputs = decoder_dense(outputs)
      # Store the current prediction (we will concatenate all predictions later)
      all_outputs.append(outputs)
      # Reinject the outputs as inputs for the next loop iteration
      # as well as update the states
      inputs = outputs
      states = [state_h, state_c]

  # Concatenate all predictions such as [batch_size, timesteps, features]
  decoder_outputs = Lambda(lambda x: K.concatenate(x, axis=1))(all_outputs)

  # Define and compile model 
  model = Model(encoder_inputs, decoder_outputs, name='model_encoder_decoder')
  model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
  return model

Let’s create the model by calling the function and check the model summary & plot

batch_size = 10
model_encoder_decoder=create_hard_coded_decoder_input_model(batch_size=batch_size)
model_encoder_decoder.summary()
plot_model(model_encoder_decoder, show_shapes=True)Model: "model_encoder_decoder"
__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
encoder_inputs (InputLayer)     [(None, 4, 10)]      0                                            
__________________________________________________________________________________________________
encoder_lstm (LSTM)             [(None, 16), (None,  1728        encoder_inputs[0][0]             
__________________________________________________________________________________________________
tf_op_layer_MatMul_1 (TensorFlo [(None, 64)]         0           encoder_lstm[0][1]               
__________________________________________________________________________________________________
tf_op_layer_AddV2_2 (TensorFlow [(10, 64)]           0           tf_op_layer_MatMul_1[0][0]       
__________________________________________________________________________________________________
tf_op_layer_BiasAdd_1 (TensorFl [(10, 64)]           0           tf_op_layer_AddV2_2[0][0]        
__________________________________________________________________________________________________
tf_op_layer_split_1 (TensorFlow [(10, 16), (10, 16), 0           tf_op_layer_BiasAdd_1[0][0]      
__________________________________________________________________________________________________
tf_op_layer_Sigmoid_4 (TensorFl [(10, 16)]           0           tf_op_layer_split_1[0][1]        
__________________________________________________________________________________________________
tf_op_layer_Sigmoid_3 (TensorFl [(10, 16)]           0           tf_op_layer_split_1[0][0]        
__________________________________________________________________________________________________
tf_op_layer_Tanh_2 (TensorFlowO [(10, 16)]           0           tf_op_layer_split_1[0][2]        
__________________________________________________________________________________________________
tf_op_layer_Mul_3 (TensorFlowOp [(10, 16)]           0           tf_op_layer_Sigmoid_4[0][0]      
                                                                 encoder_lstm[0][2]               
__________________________________________________________________________________________________
tf_op_layer_Mul_4 (TensorFlowOp [(10, 16)]           0           tf_op_layer_Sigmoid_3[0][0]      
                                                                 tf_op_layer_Tanh_2[0][0]         
__________________________________________________________________________________________________
tf_op_layer_AddV2_3 (TensorFlow [(10, 16)]           0           tf_op_layer_Mul_3[0][0]          
                                                                 tf_op_layer_Mul_4[0][0]          
__________________________________________________________________________________________________
tf_op_layer_Sigmoid_5 (TensorFl [(10, 16)]           0           tf_op_layer_split_1[0][3]        
__________________________________________________________________________________________________
tf_op_layer_Tanh_3 (TensorFlowO [(10, 16)]           0           tf_op_layer_AddV2_3[0][0]        
__________________________________________________________________________________________________
tf_op_layer_Mul_5 (TensorFlowOp [(10, 16)]           0           tf_op_layer_Sigmoid_5[0][0]      
                                                                 tf_op_layer_Tanh_3[0][0]         
__________________________________________________________________________________________________
tf_op_layer_packed (TensorFlowO [(1, 10, 16)]        0           tf_op_layer_Mul_5[0][0]          
__________________________________________________________________________________________________
tf_op_layer_Transpose (TensorFl [(10, 1, 16)]        0           tf_op_layer_packed[0][0]         
__________________________________________________________________________________________________
decoder_dense (Dense)           (10, 1, 10)          170         tf_op_layer_Transpose[0][0]      
                                                                 decoder_lstm[0][0]               
                                                                 decoder_lstm[1][0]               
                                                                 decoder_lstm[2][0]               
__________________________________________________________________________________________________
decoder_lstm (LSTM)             [(10, 1, 16), (10, 1 1728        decoder_dense[0][0]              
                                                                 tf_op_layer_Mul_5[0][0]          
                                                                 tf_op_layer_AddV2_3[0][0]        
                                                                 decoder_dense[1][0]              
                                                                 decoder_lstm[0][1]               
                                                                 decoder_lstm[0][2]               
                                                                 decoder_dense[2][0]              
                                                                 decoder_lstm[1][1]               
                                                                 decoder_lstm[1][2]               
__________________________________________________________________________________________________
lambda (Lambda)                 (10, 4, 10)          0           decoder_dense[0][0]              
                                                                 decoder_dense[1][0]              
                                                                 decoder_dense[2][0]              
                                                                 decoder_dense[3][0]              
==================================================================================================
Total params: 3,626
Trainable params: 3,626
Non-trainable params: 0
__________________________________________________________________________________________________

Train model

model_encoder_decoder.fit(X_train, y_train,
          batch_size=batch_size,
          epochs=30,
          validation_split=0.2)

We can run the compiled model as shown above. However, I will use the auxiliary function “train_test()” that I prepared for caring training and testing of a given model with the Early Stopping mechanism.

IMPORTANT: You can access and check train_test() function & the full code on Colab.

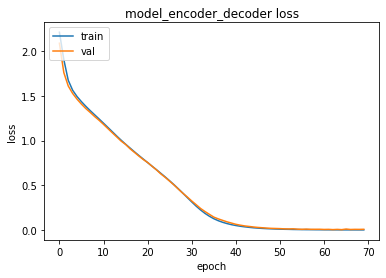
train_test(model_encoder_decoder, X_train, y_train , X_test, 	y_test, batch_size=batch_size,epochs=500, verbose=1)training for  500  epochs begins with EarlyStopping(monitor= val_loss, patience= 5 )....
Epoch 1/500
180/180 [==============================] - 2s 11ms/step - loss: 2.2124 - accuracy: 0.2200 - val_loss: 2.0893 - val_accuracy: 0.3038
....Epoch 70/500
180/180 [==============================] - 1s 4ms/step - loss: 6.6901e-04 - accuracy: 1.0000 - val_loss: 0.0076 - val_accuracy: 0.9975
Epoch 00070: early stopping
500  epoch training finished...

PREDICTION ACCURACY (%):
Train: 99.975, Test: 99.750

10 examples from test data...
Input          Expected       Predicted         T/F
[2, 1, 4, 2]   [2, 4, 1, 2]   [2, 4, 1, 2]   True
[6, 5, 1, 6]   [6, 1, 5, 6]   [6, 1, 5, 6]   True
[6, 4, 9, 1]   [1, 9, 4, 6]   [1, 9, 4, 6]   True
[2, 5, 8, 7]   [7, 8, 5, 2]   [7, 8, 5, 2]   True
[5, 2, 9, 7]   [7, 9, 2, 5]   [7, 9, 2, 5]   True
[4, 2, 3, 1]   [1, 3, 2, 4]   [1, 3, 2, 4]   True
[2, 2, 9, 3]   [3, 9, 2, 2]   [3, 9, 2, 2]   True
[5, 6, 9, 7]   [7, 9, 6, 5]   [7, 9, 6, 5]   True
[3, 8, 7, 1]   [1, 7, 8, 3]   [1, 7, 8, 3]   True
[9, 1, 3, 9]   [9, 3, 1, 9]   [9, 3, 1, 9]   True
Accuracy:  1.0

OBSERVATIONS

We use LSTM as the Recurrent Neural Network in the model
We set LSTM parameters: return_sequences and return_state according to the design of the Encoder-Decoder model
We implement the model with a single LSTM layer in the Encoder and Decoder parts.
We created an encoder-decoder model for fixed-size input/output sequences
The encoder consumes all the input sequences and creates a context vector
The decoder uses the context vector created by the Encoder and a special sign ‘START’ to output the initial token in the output sequence
The decoder works in a loop
At each cycle of the loop, the Decoder generates a token in the output sequence
To create the next token, the decoder uses its last output and last hidden & cell states as input and context vector to itself respectively
When the fixed-size output tokens are created decoder stops