LSTM: Understanding the Number of Parameters

In this tutorial, we will focus on the internal structure of the Keras LSTM layer in order to understand how many learnable parameters an LTSM layer has.

Why do we need to care about calculating the number of parameters in the LSTM layer since we can easily get this number in the model summary report?

Well, there are several reasons:

First of all, to calculate the number of learnable parameters correctly, we need to understand how LSTM is structured and how LSTM operates in depth. Thus, we will delve into LSTM gates and gate functions. We will gain precious insight into how LSTM handles time-dependent or sequence input data.
Secondly, in ANN models, a number of parameters is a really important metric for understanding the model capacity and complexity. We need to keep an eye on the number of parameters of each layer in the model to handle overfitting or underfitting situations. One way to prevent these situations is to adjust the number of parameters of each layer. We need to know how the number of parameters actually affects the performance of each layer.

If you want to enhance your understanding of the LSTM layer and learn how many learnable parameters it has please continue this tutorial.

By the way, I would like to mention that in my Youtube channel I have a dedicated playlist in English (All About LSTM) and in Turkish (LSTM Hakkında Herşey). You can check these playlists to learn more about LSTM.

Lastly, if you want to be notified of upcoming tutorials about LSTM and Deep Learning please subscribe to my Youtube channel and activate notifications.

Thank you!

Now, let’s get started!

Photo by Sigmund on Unsplash

References:

tf.keras.layers.LSTM official website

Counting No. of Parameters in Deep Learning Models by Hand by Raimi Karim

llustrated Guide to LSTM’s and GRU’s: A step by step explanation by Michael Phi

Animated RNN, LSTM and GRU by Raimi Karim

Number of parameters in Keras LSTM by Dejan Batanjac

REMINDER:

LSTM expects input data to be a 3D tensor such that:
[batch_size, timesteps, feature]
batch_size how many samples in each batch during training and testing
timesteps means how many values exist in a sequence. For example in [4, 7, 8, 4] there are 4 timesteps
features: how many dimensions are used to represent a data in one time step. For example, if each value in the sequence is one hot encoded with 9 zero and 1 one then feature is 10
Example:
In raw format:
X=[4, 7, 8, 4]
In one hot encoded format with 10 dimensions (feature = 10):
X=[[0 0 0 0 1 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 0 0 0 0]]

A Sample LSTM Model

By the way, you can access this Colab Notebook from the link.

# define model
timesteps=40         # dimensionality of the input sequence
features=3           # dimensionality of each input representation                     
                     # in the sequence
LSTMoutputDimension = 2 # dimensionality of the LSTM outputs (Hidden 
                        #  & Cell states)

input = Input(shape=(timesteps, features))
output= LSTM(LSTMoutputDimension)(input)
model_LSTM = Model(inputs=input, outputs=output)

model_LSTM.summary()Model: "functional_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         [(None, 4, 3)]            0         
_________________________________________________________________
lstm (LSTM)                  (None, 2)                 48        
=================================================================
Total params: 48
Trainable params: 48
Non-trainable params: 0
_________________________________________________________________

FINDING NUMBER OF PARAMETERS IN A NEURAL NETWORK WITH A SINGLE DENSE LAYER

Before explaining how to calculate number of LSTM parameters, I would like to remind you how to calculate number of a dense layer’s parameters. *As we will see soon, LSTM has 4 dense layers in its internal structure. So this discussion will help us a lot soon. *Assume that

i= input size

h= size of hidden layer (number of neurons in the hidden layer)

o= output size (number of neurons in the output layer)

For a single hidden layer,
number of parameters in the model = connections between layers + biases in every layer (hiden + output layers!)
= (i×h + h×o) + (h+o)
Check the below Figure taken from here

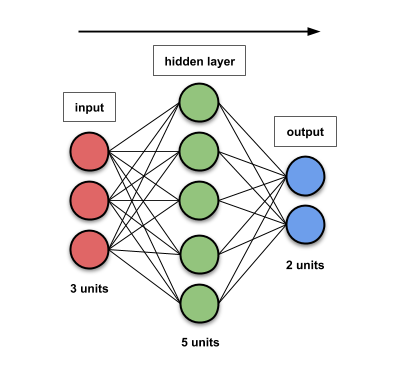
We can find the number of parameters by counting the number of connections between layers and by adding bias.

connections (weigths) between layers:
between input and hidden layer is
i * h = 3 * 5 = 15
between hidden and output layer is
h * o = 5 * 2 = 10
biases in every layer
biases in hidden layer
h = 5
biases in output layer
o = 2
Total:
15 + 10 + 5 + 2 = 32 parameters (weights + biases)

Let’s create a simple model and verify the calculation:

input = Input((None, 3))
dense = Dense(5)(input)
output = Dense(2)(dense)
model_dense = Model(input, output)
model_dense.summary()Model: "functional_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_2 (InputLayer)         [(None, None, 3)]         0         
_________________________________________________________________
dense (Dense)                (None, None, 5)           20        
_________________________________________________________________
dense_1 (Dense)              (None, None, 2)           12        
=================================================================
Total params: 32
Trainable params: 32
Non-trainable params: 0
_________________________________________________________________

Let’s re-formulate the calculations:

= (i × h + h × o) + (h + o)

= (i + o) × h + (h + o)

We will use above formula below :)

KERAS LSTM CELL STRUCTURE

Image from here

FIRST EXPLANATION USING LSTM INTERNAL STRUCTURE

Review the above Figure to capture the internal structure of LSTM cell

There are 3 inputs to the LSTM cell:
$h_{t-1}$ previous timestep (t-1) Hidden State value
$c_{t-1}$ previous timestep (t-1) Cell State value
$x_{t}$ current timestep (t) Input value
There are 4 dense layers:
Forget Gate
Input Gates = Input + Candidate
Output Gate
The input output tensor sizes (dimensions) are symbolized with circles. In the figure,
Cell and Hidden states are vectors which have a dimension = 2. This number is defined by the programmer by setting LSTM parameter units (LSTMoutputDimension) to 2
Input is a vector which has a dimension = 3. This number is also defined by the programmer by deciding how many dimension would be to represent an input (e.g. dimension of one-hot encoding, word embedding, etc.)
Note that, By definition:
Hidden and Cell states vector dimensions must be the same
Hidden and Cell states vector dimensions at time t-1 and t must be the same
Each input in the sequence must have the same vector dimensions

Let’s focus on Forget Gate

As seen in above figure,
there are Hidden state values (2 $h_{t-1}$ red circles) and
Input values ( 3 $x_{t}$ green circles)
Total 5 numbers ( 2 $h_{t-1}$ + 3 $x_{t}$ ) are inputted to a dense layer
Output layer has 2 values (which must be equal to the dimension of $h_{t-1}$ Hidden state vector in the LSTM Cell)
We can calculate the number of parameters in this dense layer as we did before:
= ($h_{t-1}$ + $x_{t}$) × $h_{t-1}$ + $h_{t-1}$
= (2 + 3) × 2 + 2
= 12
Thus Forget Gate has 12 parameters (weights + biases)

Image from here

Since there are 4 gates in the LSTM unit which have exactly the same dense layer architecture, there will be
= 4 × 12
= 48 parameters
We can formulate the parameter numbers in a LSTM layer given that $x$ is the input dimension, $h$ is the number of LSTM units / cells / latent space / output dimension:

LSTM parameter number = 4 × (($x$ + $h$) × $h$ +$h$)

SECOND EXPLANATION USING LSTM FUNCTION DEFINITIONS

The outputs of the 4 gates in the above figure can be expressed as a function as below:

As seen, among these functions, there are 4 functions which have
2 weight matrices: $W$ and $U$ for $h_{t-1}$ and $x_{t}$ values
1 bias vector $b$
We can work on forget gate’s function $f_{t}$ to calculate parameter numbers:

Notice that we can guess the size (shape) of W,U and b given:

Input size ($h_{t-1}$ and $x_{t}$ )
Output size ($h_{t-1}$)

Since output must equal to Hidden State (hx1) size:

for W param = ($h$ × $x$)
for U param = ($h$ × $h$)
for Biases param = $h$
total params = W param + U param + Biases param
= ($h$ × $x$) + ($h$ × $h$) + $h$
= ( ($h$ × $x$) + ($h$ × $h$) + $h$ )
= ( ($x$ + $h$) × $h$ + $h$ )
there are 4 functions which are exactly defined in the same way, in the LSTM layer, there will be

LSTM parameter number = 4 × (($x$ + $h$) × $h$ +$h$)

Example

# define model
timesteps=40          # dimensionality of the input sequence
features=3            # dimensionality of each input representation in the sequence
LSTMoutputDimension = 2 # dimensionality of the LSTM outputs (Hidden & Cell states)


input = Input(shape=(timesteps, features))
output= LSTM(LSTMoutputDimension)(input)
model_LSTM = Model(inputs=input, outputs=output)

model_LSTM.summary()Model: "functional_9"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_5 (InputLayer)         [(None, 40, 3)]           0         
_________________________________________________________________
lstm_3 (LSTM)                (None, 2)                 48        
=================================================================
Total params: 48
Trainable params: 48
Non-trainable params: 0
_________________________________________________________________

In the above model,

LSTM layer has “dimensionality of the output space” (unit) parameter value 2 which means that Hidden and Cell states are vectors with dimension 2
input for each time step is represented by a vector with dimension 3 (feature)

Remember:

LSTM parameter number = 4 × (($x$ + $h$) × $h$ + $h$)

LSTM parameter number = 4 × ((3 + 2) × 2 + 2)

LSTM parameter number = 4 × (12)

LSTM parameter number = 48

The summary indicates the total number of parameters of the model (actually the LSTM layer) is 48 as we computed above!

Now, let’s get sizes of each weight matrix and bias vector from the model:

W = model_LSTM.layers[1].get_weights()[0]
U = model_LSTM.layers[1].get_weights()[1]
b = model_LSTM.layers[1].get_weights()[2]

print("W", W.size, ' calculated as 4*features*LSTMoutputDimension ', 4*features*LSTMoutputDimension)
print("U", U.size, ' calculated as 4*LSTMoutputDimension*LSTMoutputDimension ', 4*LSTMoutputDimension*LSTMoutputDimension)
print("b", b.size , ' calculated as 4*LSTMoutputDimension ', 4*LSTMoutputDimension)
print("Total Parameter Number: W+ U + b " , W.size+ U.size + b.size)
print("Total Parameter Number: 4 × ((x + h) × h +h) " , 4* ((features+LSTMoutputDimension)*LSTMoutputDimension+LSTMoutputDimension))W 24  calculated as 4*features*LSTMoutputDimension  24
U 16  calculated as 4*LSTMoutputDimension*LSTMoutputDimension  16
b 8  calculated as 4*LSTMoutputDimension  8
Total Parameter Number: W+ U + b  48
Total Parameter Number: 4 × ((x + h) × h +h)  48

NOTICE:

The above W, U, and B are compacted for all gates.
If you want, you can access the values of each gate values as well:

units=LSTMoutputDimension
W_i = W[:, :units]
W_f = W[:, units: units * 2]
W_c = W[:, units * 2: units * 3]
W_o = W[:, units * 3:]

U_i = U[:, :units]
U_f = U[:, units: units * 2]
U_c = U[:, units * 2: units * 3]
U_o = U[:, units * 3:]

b_i = b[:units]
b_f = b[units: units * 2]
b_c = b[units * 2: units * 3]
b_o = b[units * 3:]

IMPORTANT:

timesteps (or input_length) of the input sequence do NOT affect the number of parameters!
WHY?
Because, the same “W”, “U”, and “b” are shared throughout the time-steps
That is; instead of using new weights and biases at each time step, the LSTM unit uses the same “W”, “U”, and “b” values for all time steps!
This simplifies the calculation of backpropagation and reduces the number of parameters (memory requirement)

CONCLUSION

In this tutorial, we investigate the internal structure of Keras LSTM layer to calculate the number of learnable parameters.
We examine several concepts: time steps, dimensionality of the output space, gates, gate functions, etc.
We come up with the correct formulation in 2 different ways:
LSTM parameter number = 4 × (($x$ + $h$) × $h$ + $h$)
We check the correctness of the formulation by creating a simple LSTM model

From here, you can continue learning about LSTM for example with understanding the outputs of LSTM layer. I have a tutorial for it already on Youtube and Medium.

Enjoy!

BONUS: Shapes of Matrices and Vectors:

# define model
timesteps=40
features=3
LSTMoutputDimension = 2

input = Input(shape=(timesteps, features))
output= LSTM(LSTMoutputDimension)(input)
model_LSTM = Model(inputs=input, outputs=output)

W = model_LSTM.layers[1].get_weights()[0]
U = model_LSTM.layers[1].get_weights()[1]
b = model_LSTM.layers[1].get_weights()[2]print("Shapes of Matrices and Vecors:")
print("Input [batch_size, timesteps, feature] ", input.shape)
print("Input feature/dimension (x in formulations)", input.shape[2])
print("Number of Hidden States/LSTM units (cells)/dimensionality of the output space (h in formulations)", LSTMoutputDimension)
print("W", W.shape)
print("U", U.shape)
print("b", b.shape)Shapes of Matrices and Vecors:
Input [batch_size, timesteps, feature]  (None, 40, 3)
Input feature/dimension (x in formulations) 3
Number of Hidden States/LSTM units (cells)/dimensionality of the output space (h in formulations) 2
W (3, 8)
U (2, 8)
b (8,)

Why 8?

Remember the functions? Examine Forget gate function below:

W matrix multiplies input vector (x) whose dimension in the example is 1x3 to produce results as many as hidden states which is 2 in the example.
Thus, it is expected that W dimension should be 3x2 but why 3x8?
Because there are 4 gates/functions! and W is the matrix for the whole layer!
Therefore, W dimension is 3 x (2 x 4) = 3 x 8!
Above fact also explains why U and b has 8 values

= 4 * number of hidden states!

We can formulate the dimensions of parameters as:

W [ x , 4 * h ]

U [ h , 4 * h ]

b [ 4 * h ]

where

**x** is the number of dimension/feature of the input

**h** is the number of Hidden States/LSTM units (cells)/dimensionality of the output space

You can follow me on these social networks:

Thursday, November 10, 2022